Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 편미분
- 교차 엔트로피
- 파이썬 날코딩으로 알고 짜는 딥러닝
- 자료구조
- 인공지능
- 파이썬 딥러닝
- lost function
- 자연어처리
- 퍼셉트론
- 순차 자료구조
- DB
- 오퍼랜드
- 선형 리스트
- 뇌를 자극하는 알고리즘
- 딥러닝
- 노드
- 파라미터
- 컴퓨터구조
- 단층퍼셉트론
- 확률분포
- 연결 자료구조
- 회귀분석
- 딥러닝 교차엔트로피
- 엔트로피
- 신경망
- DBMS
- 자료구조 알고리즘
- 딥러닝 교차 엔트로피
- 리스트
- 단층 퍼셉트론
Archives
- Today
- Total
YZ ZONE
[ 자료구조 및 알고리즘 ] 4. 순차 자료구조 - 3. 다항식의 순차 자료구조 표현 본문
다항식
aX^e 형식의 항들의 합으로 구성된 식
• a : 계수(coefficient)
• X : 변수(variable)
• e : 지수(exponent)
다항식의 특징
• 지수에 따라 내림차순으로 항을 나열
• 다항식의 차수 : 가장 큰 지수
• 다항식 항의 최대 개수 = (차수 +1)개
다항식의 추상 자료형


다항식의 표현
각 항의 지수와 계수의 쌍에 대한 선형 리스트
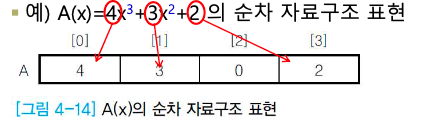
• 예) A(x)=4x3+3x2+2 ☞ p1= (3,4, 2,3, 0,2)
1차원 배열을 이용한 순차 자료구조 표현
차수가 n인 다항식을 (n+1)개의 원소를 가지는 1차원 배열로 표현
배열 인덱스 i : 지수(n-i)을 의미
배열 인덱스 i의 원소 : 지수(n-i)항의 계수
• 다항식에 포함되지 않은 지수의 항에 대한 원소에 0 저장



차수가 1000이므로 크기가 1001인 배열을 사용하는데, 항이 3개 뿐이므로 배열의 원소 중에서 3개만 사용
☞ 998개의 배열 원소에 대한 메모리 공간 낭비!
» 지수와계수를표현할방법필요⇒2차원배열도한가지방법임
2차원 배열을 이용한 순차 자료구조 표현
다항식의 각 항에 대한 <지수, 계수>의 쌍을 2차원 배열에 저장
• 2차원 배열의 행의 개수 : 다항식의 항의 개수
• 2차원 배열의 열의 개수 : 2
• 예) B(x)=3x1000 + x + 4 의 2차원 배열 표현
− 1차원 배열을 사용하는 방법보다 메모리 사용 공간량 감소
☞공간복잡도감소 ☞프로그램성능향상!


publicclassEx5_4{
public static void main(String args[]){
float a[]= new float[] {4,3,5,0};
float b[]= new float[] {3,1,0,2,1};
Polynomial A = new Polynomial(3, a);
Polynomial B = new Polynomial(4, b);
OperatePoly optPoly = new OperatePoly();
Polynomial C = optPoly.addPoly(A,B);
System.out.printf("A(x)="); A.printPoly();
System.out.printf("B(x)="); B.printPoly();
System.out.printf("C(x)="); C.printPoly();
}
}
classOperatePoly{
private int degree_A=0, degree_B=0, degree_C=0, index_A=0,index_B=0, index_C=0;
private int expo_A, expo_B;
private float coef_A, coef_B, coef_C;
publicPolynomialaddPoly(PolynomialA,PolynomialB){
degree_A = A.getDegree();
degree_B = B.getDegree();
expo_A = degree_A;
expo_B = degree_B;
if(degree_A >= degree_B) degree_C=degree_A;
else degree_C=degree_B;
Polynomial C = new Polynomial(degree_C);
while(index_A <= degree_A && index_B <= degree_B){
if(expo_A > expo_B){
C.setCoef(index_C++, A.getCoef(index_A++));
expo_A--;
}
else if(expo_A == expo_B){
C.setCoef(index_C++, A.getCoef(index_A++)+ B.getCoef(Index_B++));
expo_A--; expo_B--;
}
else {
C.setCoef(index_C++, B.getCoef(index_B++));
expo_B--;
}
}
return C;
}
}
class Polynomial{
private int degree;
private float coef[]=new float[20];
Polynomial (int degree, float coef[]){
this.degree = degree;
this.coef = coef;
}
Polynomial (int degree){
this.degree = degree;
for(int i=0; i<=degree; i++)
this.coef[i] = 0;
}
public int getDegree(){
return this.degree;
}
public float getCoef(int i){
return this.coef[i];
}
public float setCoef(int i,float coef){
return this.coef[i]=coef;
}
public void printPoly(){
int temp= this.degree;
for(int i=0; i<=this.degree; i++){
System.out.printf("%3.0fx^%d", this.coef[i], temp--);
}
System.out.println();
}
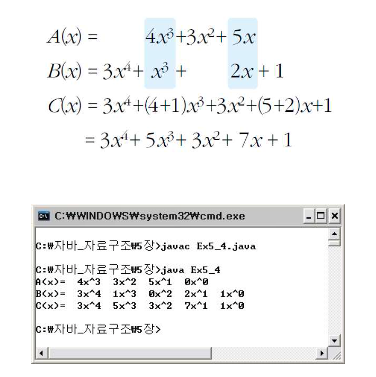
}실행 결과
'IT > 자료구조 및 알고리즘' 카테고리의 다른 글
| [ 자료구조 및 알고리즘 ] 5.연결 자료구조 - 1.연결 자료구조 (0) | 2023.02.24 |
|---|---|
| [ 자료구조 및 알고리즘 ] 4. 순차 자료구조 - 4. 행렬의 순차 자료구조 표현 (1) | 2023.02.23 |
| [ 자료구조 및 알고리즘 ] 4. 순차 자료구조 - 2. 선형 리스트의 구현 (0) | 2023.02.23 |
| [ 자료구조 및 알고리즘 ] 4. 순차 자료구조 - 1.선형 리스트 (0) | 2023.02.18 |
| [뇌를 자극하는 알고리즘] 5. 정렬 (0) | 2022.02.19 |




