Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 파이썬 딥러닝
- 오퍼랜드
- 연결 자료구조
- 신경망
- 순차 자료구조
- 자료구조 알고리즘
- 자료구조
- 회귀분석
- 단층 퍼셉트론
- 노드
- 교차 엔트로피
- 단층퍼셉트론
- 딥러닝 교차엔트로피
- 확률분포
- DBMS
- 퍼셉트론
- 편미분
- DB
- 인공지능
- lost function
- 리스트
- 딥러닝
- 뇌를 자극하는 알고리즘
- 파이썬 날코딩으로 알고 짜는 딥러닝
- 자연어처리
- 선형 리스트
- 엔트로피
- 파라미터
- 컴퓨터구조
- 딥러닝 교차 엔트로피
Archives
- Today
- Total
YZ ZONE
[자연어처리] 2.6 자연어처리를 위한 수학(최적화) 본문
2.3 최적화
순수 수학의 최적화: 어떤식이 있을때 최적점을 찾는것.
기계학습의 최적화: 훈련집합이라는 샘플 데이터가 일정한 양이 주어지고, 그 집합에 따라 정해지는 목적 함수의 최저점을 찾아야함.
어떻게 찾냐? 뒤에서 배움.
-데이터로 미분하는 과정 필요→오류 역전파 알고리즘(3.4절)
-주로 SGD(스토캐스틱 경사 하강법)사용
2.3.1 매개변수 공간의 탐색
데이터가 있을때 데이터가 발생하는 특징공간에서 확률분포를 정확하게 추론을 할 수 있으면 분류를 정화하게 할 수 있게 됨. 기계학습에서는 학습 데이터(학습, 훈련집합에 사용되어지는 작은 양의 데이터)를 통해서 찾아내야하는 문제가 있음. 실제 특징공간에서의 차원은 매우 큰데 그에 비해 훈련집합의 크기는 작아 참인 확률분포를 구하는 일은 불가능함.
따라서 기계학습은 적절한 모델을 선택해 목적함수를 정의하고, 모델의 매개변수 공간을 탐색하여 목적함수의 최저점을 찾는 전략 사용.
즉 특징 공간에서 해야 하는 일을 모델의 매개변수 공간에서 하는 일로 대치하여 처리를 한다.
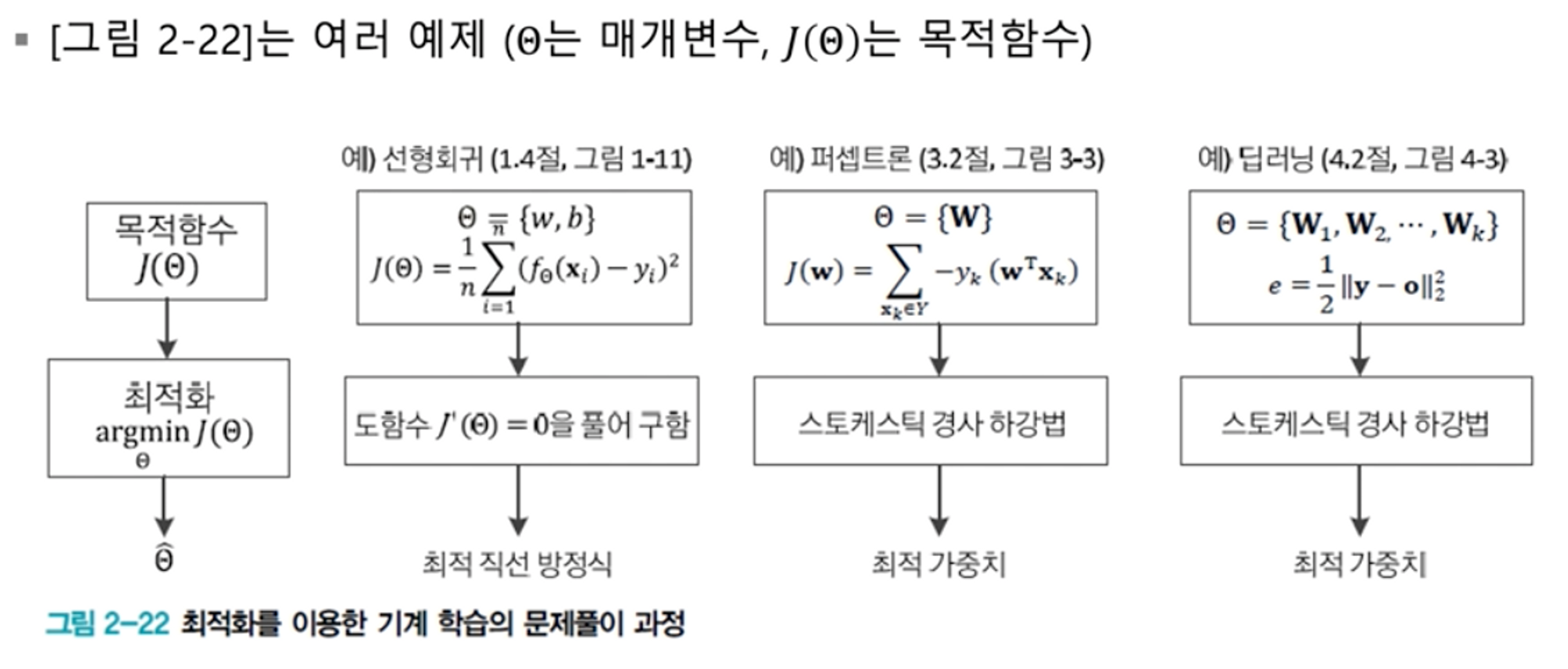
목적함수가 최저값이 되도록하는 세타(매개변수)를 계속 변경해 찾는것이(최적화 argmin) 기계학습에서 하고자하는 일.
학습모델의 매개변수 공간은 특징 공간보다 훨씬 넓다.


목적함수가 작아지는 방향으로 미분으로 찾아냄
세타를 넣어 작아지는 방향을 구함. 구한 만큼을 세타에 다시 더해 값을 작아지는 방향으로 값을 몰아가 찾음.

'IT > 자연어처리' 카테고리의 다른 글
| [자연어처리] 2. 자연어처리를 위한 수학-복습2 (0) | 2023.02.02 |
|---|---|
| [자연어처리] 2. 자연어처리를 위한 수학-복습 (0) | 2023.02.02 |
| [자연어처리] 2.5 자연어처리를 위한 수학(정보이론) (0) | 2023.02.02 |
| [자연어처리] 2.4 자연어처리를 위한 수학(평균과 분산) (0) | 2023.02.02 |
| [자연어처리] 2.3 자연어처리를 위한 수학(최대우도) (0) | 2023.02.02 |




