Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 파이썬 날코딩으로 알고 짜는 딥러닝
- 파라미터
- 오퍼랜드
- 파이썬 딥러닝
- 편미분
- 노드
- 선형 리스트
- DB
- 딥러닝 교차 엔트로피
- 딥러닝
- 자료구조
- lost function
- 확률분포
- 컴퓨터구조
- 단층퍼셉트론
- 교차 엔트로피
- DBMS
- 회귀분석
- 자료구조 알고리즘
- 리스트
- 인공지능
- 뇌를 자극하는 알고리즘
- 자연어처리
- 엔트로피
- 퍼셉트론
- 딥러닝 교차엔트로피
- 연결 자료구조
- 신경망
- 순차 자료구조
- 단층 퍼셉트론
Archives
- Today
- Total
YZ ZONE
[딥러닝] 1. 단층 퍼셉트론(SLP) _ 1. 회귀분석_ 1.6 경사하강법과 역전파 본문
정답과 추정한 값의 차이를 줄여나가는 것이 학습의 과정인데 이것을 경사하강법으로 찾아나감.
경사하강법 gradient descent algorithm
- w(weight)값을 조정해나가는 일종의 전략
- 딥러닝의 가장 기본적인 학습 알고리즘
- 함수의 기울기 계산해 함숫값이 작아지는 방향으로 이동 반복
- 미니배치 입력에 대해 순전파와 역전파를 번갈아 반복 수행
→ 입력 넣고 출력이 나왔을때 출력과 정답의 차이를 미분을 통해 기울기로 구해 얼만큼 하강시켜야 하는지 기울기를 계산해 w를 수정해 나감
→ 이 과정을 기울기가 작아질때까지 출력과 정답의 차이가 거의 나지 않을 때까지 반복
순전파: 입력 정보로부터 손실 함수 계산 과정
- 신경망 구조를 따라가면서 현재의 파라미터값 이용해 계산
역전파
- 정답과 출력한 추정(예측)값의 차이를 계산해 w에 반영
- 순전파 계산 과정의 역순으로 진행
- 손실 함숫값에 영향 미친 모든 성분에 대해 손실 기울기 계산
- 파라미터 성분의 경우 계산된 손실 기울기 이용해 값을 변경
이 변경이 바로 신경망 변화를 가져오는 학습의 핵심 과정
학습률 hyper parameter
: 차이의 기울기를 계산한 에 비례해 w를 수정할것인데 비율을 얼마만큼씩 반영 할 것이냐.
- 학습 속도를 조절하는 하이퍼 파라미터
하이퍼 파라미터: 모델 파라미터(w)와는 다름. 우리가 임의로 직접 정해줘야 하는 것. 학습률, 노드의 개수, 히든레이어 수 등
- 파라미터값 = 파라미터값 - 학습률 x 손실기울기
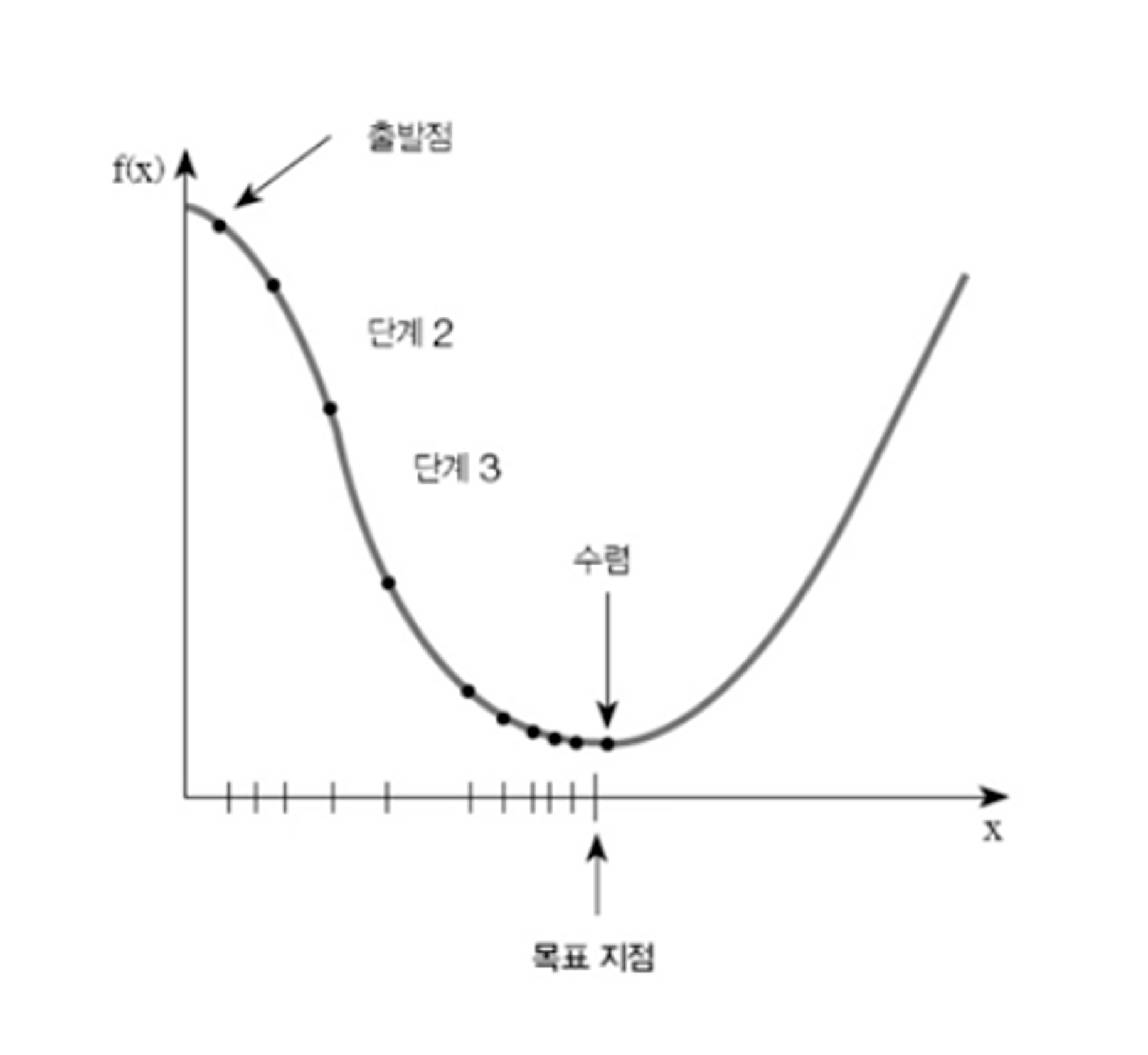
출발점에서 바닥의 목표지점을 찾아가기
- 그래프 전체를 볼 수 없는 상황 전제
- 경사가 심할수록 바닥이 멀리 있으니 빨리 내려가도 된다
→경사가 완만하면 목표 지점 지나치지 않도록 천천히 이동
즉 초반에 정답과 추정값의 차이가 많이나 경사가 심하면 빠르게 이동을 해야하기 때문에 학습률을 높여 많이 반영하고 목표 지점으로 가까워질수록 경사가 완만해지고 세밀하게 이동해야 하기에 학습률을 적게 조정한다.
- 경사가 오르막이라면 후진
→경사가 내리막이면 전진
그래프의 경사는 미분값에 해당
- 경사에 비례하는 값을 x에서 빼주면 모든 처리 가능
편미분 Partial
- 경사하강법에서는 전미분 대신 편미분 사용
- 전미분: 다른 변수 통한 간접 효과까지 모두 고려하는 미분법
- 편미분: 관심 변수 외의 변수를 모두 상수 취급하는 간단한 미분법
- 편미분은 전미분에 비해 훨씬 쉽게 계산할 수 있다.
- 상수 취급되는 다른 변수도 값은 편미분 방식으로 처리해 총합
전체적으로 전미분에 준하는 효과를 기대할 수 있다.

우리는 경사하강법을 하기 위해서 기울기를 측정하는데 편미분을 한다.
경사하강법과 등산로
- 손실함숫값 최소화: 등산로에서 바닥점 찾아가기로 비유 가능
- 손실 함숫값을 결정하는 성분은 신경망 안의 수많은 파라미터들
- 가능한 파라미터 값의 조합: R^n 다차원 공간
전체 경우를 계산해 최소값 찾는 것은 현실적으로 불가능
수학적으로 풀어내 최소값 찾는 것도 현실적으로 불가능
- 현재 위치에서 기울기 따져가며 한 걸음씩 하강 불가피
경사하강법이 찾아내는 경로
- 등산객의 안전한 하산경로보다 물이 흘러가는 경로와 비슷
지역적 바닥점 문제
- 경사하강법으로 바닥 지점에 도달할 수 있다는 보장은 없다.
- 현재위치 주변 지형에 따라 지역적 바닥점에 도달할 가능성 상존
- 지역적 바닥점 문제에 대한 근본적인 해결책은 아직 없다.
'IT > 딥러닝' 카테고리의 다른 글
| [딥러닝] 1. 단층 퍼셉트론(SLP) _ 1. 회귀분석_ 1.8 하이퍼파라미터 (0) | 2023.07.28 |
|---|---|
| [딥러닝] 1. 단층 퍼셉트론(SLP) _ 1. 회귀분석_ 1.7 편미분과 손실기울기 계산 (0) | 2023.07.28 |
| [딥러닝] 1. 단층 퍼셉트론(SLP) _ 1. 회귀분석_1.5 회귀분석과 MSE 손실함수 (0) | 2023.07.28 |
| [딥러닝] 1. 단층 퍼셉트론(SLP) _ 1. 회귀분석_ 1.3 신경망의 세 가지 출력 유형과 회귀 분석 (0) | 2023.07.26 |
| [딥러닝] 1. 단층 퍼셉트론(SLP) _ 1. 회귀분석_ 1.2 텐서 연산과 미니배치의 활용 (0) | 2023.07.26 |




